Redes Neurais – Perceptron

1. Introdução

O perceptron representa a primeira implementação bem-sucedida de um neurônio artificial capaz de aprender, servindo como base para o desenvolvimento de arquiteturas neurais mais complexas que hoje impulsionam muitas das tecnologias de inteligência artificial.

2. Definição e Contexto Histórico

2.1 Definição

O perceptron é um modelo matemático inspirado nos neurônios biológicos, projetado para realizar classificação binária através de um processo de aprendizagem supervisionada. Em sua forma mais básica, o perceptron recebe múltiplas entradas numéricas, aplica pesos a essas entradas, soma-as e produz uma saída binária com base em uma função de ativação de limiar.

2.2 Contexto Histórico

O perceptron foi concebido pelo psicólogo Frank Rosenblatt em 1957 no Laboratório Aeronáutico Cornell. Ele implementou o primeiro modelo físico em 1958, denominado Mark I Perceptron, uma máquina construída para reconhecimento de padrões visuais. O projeto foi financiado pela Marinha dos Estados Unidos e representou uma das primeiras tentativas de criar uma “máquina capaz de aprender”.

A publicação do livro “Principles of Neurodynamics” por Rosenblatt em 1962 documentou extensivamente o perceptron e suas aplicações, criando grande entusiasmo sobre as possibilidades de máquinas inteligentes.

Contudo, em 1969, Marvin Minsky e Seymour Papert publicaram o livro “Perceptrons”, onde demonstraram matematicamente as limitações do perceptron simples, particularmente sua incapacidade de resolver problemas não linearmente separáveis, como a função lógica XOR. Esta publicação causou o que ficou conhecido como o “primeiro inverno da IA”, reduzindo drasticamente o financiamento e interesse em redes neurais durante mais de uma década.

O interesse foi renovado nos anos 1980 com o desenvolvimento do algoritmo de retropropagação (backpropagation) e perceptrons multicamadas, que superaram as limitações apontadas por Minsky e Papert.

3. Estrutura e Funcionamento do Perceptron Simples

3.1. Analogia com o Neurônio Biológico

O perceptron foi inspirado na estrutura e funcionamento básico dos neurônios biológicos:

As entradas do perceptron representam os dendritos do neurônio, que recebem sinais de outros neurônios.
Os pesos correspondem às sinapses, que determinam a força da conexão entre neurônios.
A função de soma simula a integração de sinais no corpo celular do neurônio.
A função de ativação representa o processo de disparo do potencial de ação no axônio do neurônio.
A saída do perceptron equivale ao terminal axônico, que transmite o sinal para outros neurônios.

3.2. Componentes do Perceptron

Um perceptron simples consiste em:

Entradas (x₁, x₂, …, xₙ): Valores numéricos que representam os atributos do exemplo.
Pesos (w₁, w₂, …, wₙ): Valores numéricos que definem a importância de cada entrada.
Bias (b) ou peso w₀: Um termo constante que permite ajustar o limiar de ativação.
Função de soma: Calcula a soma ponderada das entradas multiplicadas pelos pesos correspondentes.
Função de ativação: Transforma a soma ponderada em uma saída binária.

3.3. Representação Matemática

O perceptron calcula uma combinação linear das entradas e aplica uma função de ativação:

Combinação linear: $$z = \sum_{i=1}^{n} w_i x_i + b = w_1x_1 + w_2x_2 + … + w_nx_n + b$$

Ou, em notação vetorial: $$z = \vec{w} \cdot \vec{x} + b$$

Onde:

$\vec{w} = [w₁, w₂, …, wₙ]$ é o vetor de pesos
$\vec{x} = [x₁, x₂, …, xₙ]$ é o vetor de entradas
$b$ é o bias

Função de ativação: No perceptron original, utiliza-se a função degrau (step function):

$f(z) = { 1, se z ≥ 0 0, se z < 0 }$

$$f(z) =
\begin{cases}
1, & \text{se } z \geq 0 \\
0, & \text{se } z < 0
\end{cases}$$

A saída final y é dada por: $$y = f(z) = f\left(\sum_{i=1}^{n} w_i x_i + b\right)$$

O que é o bias?

O bias (também chamado de viés ou termo de polarização) desempenha um papel fundamental no funcionamento do perceptron e das redes neurais em geral. Sua função principal é permitir que o perceptron se adapte melhor aos dados, aumentando sua flexibilidade e capacidade de representação.

Funções Principais do Bias:

O bias permite deslocar o hiperplano de decisão para longe da origem, sem alterar sua orientação. Em termos geométricos:

Sem bias: O hiperplano de decisão (definido por $w·x = 0$) é forçado a passar pela origem.
Com bias: O hiperplano pode ser posicionado em qualquer lugar do espaço de entrada (definido por $w·x + b = 0$).

Exemplo

Considere um problema de classificação binária simples em 2D:

Sem bias, a linha de decisão é: $w₁x₁ + w₂x₂ = 0$ (sempre passando pela origem)
Com bias, a linha de decisão é: $w₁x₁ + w₂x₂ + b = 0$ (pode ser posicionada em qualquer lugar)

Importância no Aprendizado

Durante o treinamento do perceptron, o bias é ajustado junto com os pesos usando a regra de aprendizado, permitindo que o modelo encontre a fronteira de decisão ótima para os dados de treinamento.
Sem o bias, a capacidade representacional do perceptron seria severamente limitada, impossibilitando a resolução de muitos problemas de classificação simples.

3.4. Representação Visual do Perceptron

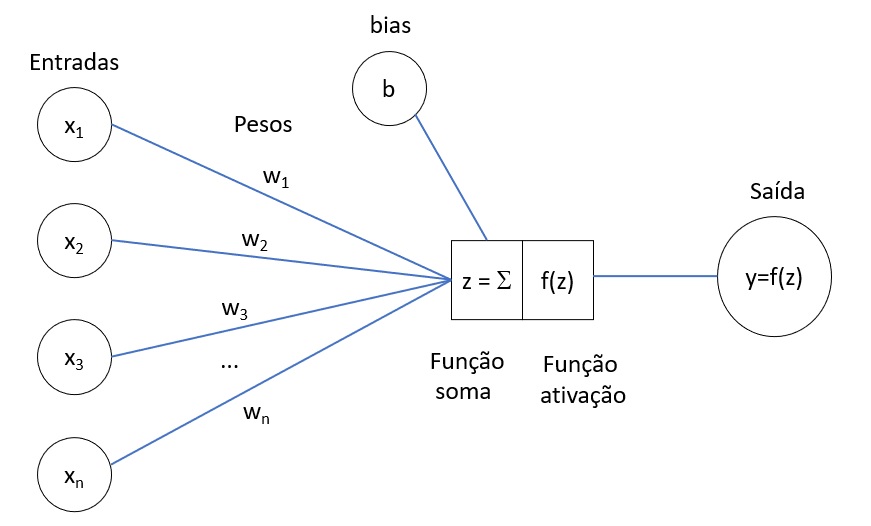
Exemplo-1:

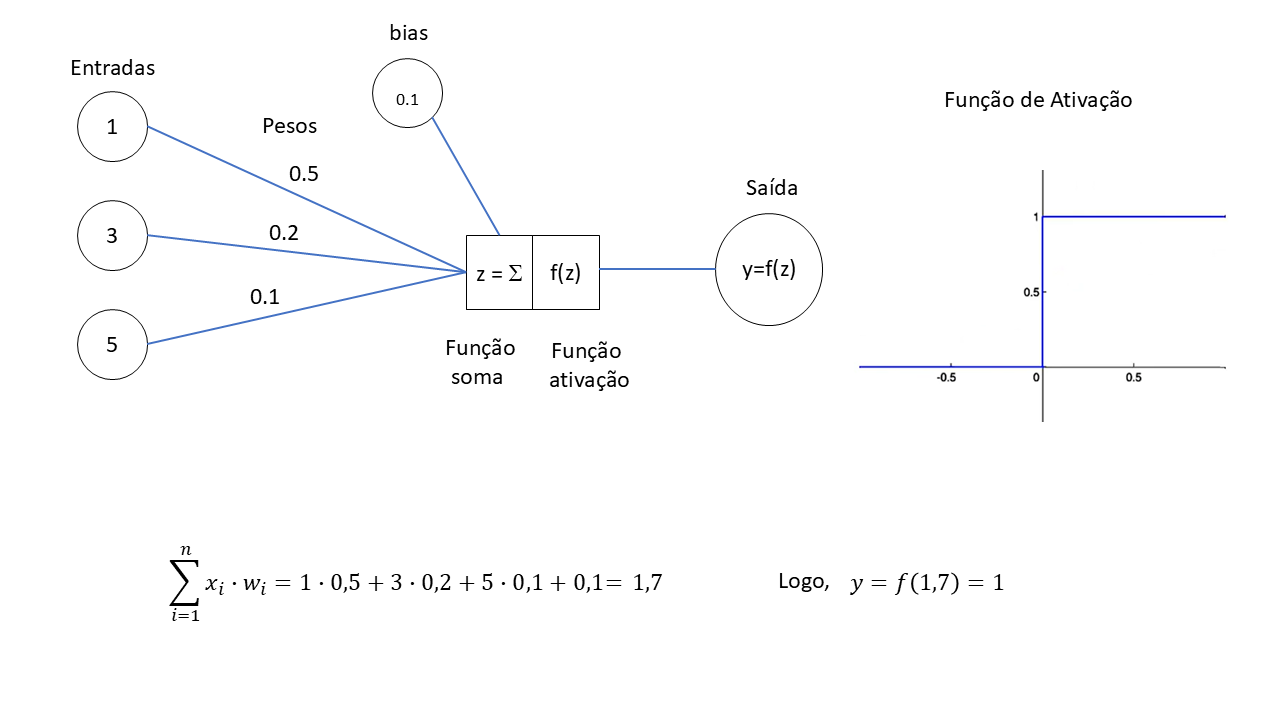
Exemplo-2:

4. Exemplo Prático: Ajuste de Peso usando a Tabela AND

Este exemplo descreve o processo de ajuste de pesos utilizando a lógica da tabela AND e a implementação em Python no ambiente Google Colab. A tabela AND será empregada como critério para determinar se um peso deve ser aumentado ou diminuído, com base na avaliação de múltiplas condições. O código Python demonstrará como representar os dados, aplicar a lógica AND para identificar os pesos a serem ajustados e realizar as modificações necessárias

Tabela AND

X1	X2	X1 AND X2
0	0	0
0	1	0
1	0	0
1	1	1

1. Inicialização dos Pesos e Bias no Perceptron

O método mais comum é o da inicialização aleatória:

Os pesos (w) são geralmente inicializados com valores aleatórios pequenos, tipicamente no intervalo $[-0.5, 0.5]$ ou $[\frac{-1}{\sqrt{n}}, \frac{-1}{\sqrt{n}}]$, onde $n$ é o número de entradas.
O $bias$ ($b$) também é inicializado aleatoriamente, frequentemente com um pequeno valor negativo (para evitar que o perceptron ative sem estímulo).

Razões para usar inicialização aleatória:

- Evita que todos os neurônios aprendam exatamente o mesmo padrão
- Permite explorar diferentes regiões do espaço de solução
- Ajuda a quebrar a simetria entre neurônios em redes mais complexas

6. Considerações Finais

A história das redes de computadores e da Internet é uma jornada de inovação contínua, desde os primeiros experimentos com a comutação de pacotes até a onipresença da Internet em nossas vidas hoje. A colaboração entre pesquisadores, empresas e governos foi fundamental para o desenvolvimento e a expansão da Internet, transformando a forma como nos comunicamos, trabalhamos e vivemos.

7. Referência Bibliográfica

KUROSE, James F.; ROSS, Keith W. Redes de computadores e a internet: uma abordagem top-down. 8. ed. São Paulo: Pearson, 2021.